The year 2022 was marked by a sharp inflationary surge in the United States and the euro zone. At the end of October, the inflation rate hit 7.7% over one year in the US, 10.6% in the euro zone and 7.1% in France, i.e. between 5 and 8 points above the inflation targets of the US Federal Reserve (Fed) and the European Central Bank (ECB). In response, the two central banks significantly tightened monetary policy. The Fed raised its key interest rate from 0% in March 2022 to 4% in November 2022. While the ECB’s key rate hike has been more measured for the moment, long-term rates on public debt in European countries have risen sharply, gaining between 250 and 300 basis points in one year in France and Germany, and even more in euro zone countries where the risk on public debt is perceived as higher. This increase is close to what is anticipated for short-term rates in 2023. The OFCE thus forecasts that the ECB’s key rate will reach 3% in the third quarter of 2023[1].
It is not easy to estimate the impact this tightening will have on economic activity. There is a very rich literature on the transmission of a monetary shock to the rest of the economy, using methods that, while conceptually similar or even equivalent, in practice lead to a wide variety of results. We are particularly interested here in the impact of a rate shock using macroeconometric models of the French economy. For this overview, we chose three models: the Mésange model co-developed by the French Treasury Dept and the INSEE statistics agency (see Bardaji et al., 2017), the FR BDF model of the Banque de France (see Lemoine et al., 2019, and Aldama and Ouvrard, 2020, for the notebook on variants), along with the OFCE e-mod model used in Heyer and Timbeau (2006).
What is a macroeconometric model?
Macroeconometric models are the oldest class of macroeconomic models. They combine accounting relationships (or equations) with estimated behavioural equations in order to make predictions about an economy’s response to shocks. The major macroeconomic variables (wages, prices, household consumption, investment, employment) are expressed in the form of error correction equations. In the long run, these converge towards a certain target, which is determined by economic theory. Thus household consumption expenditure will converge on a certain fraction of household disposable income in the long term. In contrast, short-term behaviour is left much freer in order to achieve a good forecasting performance. The interest rate is essentially a long-term factor. The impact of a rate shock is limited initially and becomes more important as the gap between the variables and their long-term targets closes.
The Mésange model
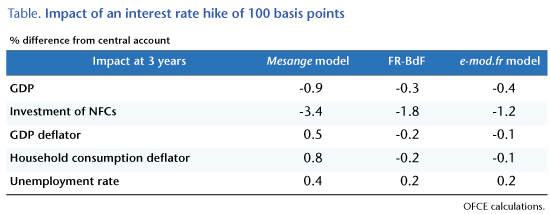
We consider the variant published in Bardaji et al. (2017). The results are summarised in Table 1. A monetary shock of 100 basis points (or 1%) results in a fall in GDP of 0.2% after one year, 0.8% after three years and 3% in the long run. This decline is due in particular to a sharp drop in investment: -2.7% after 3 years (-3.4% for the GFCF of non-financial companies) and -5.5% in the long term, but all components of aggregate demand are hit, including exports, which fall by 3.3% in the long haul. Surprisingly, monetary tightening is reflected in higher prices in the Mésange model. Value-added market prices rise by 0.1% after one year, 0.8% after three years and more than 6% over a longer period! This price increase makes the economy less competitive, hence the fall in exports. Two transmission channels are at work. The first is the direct negative impact of higher interest rates on business investment. In the Mésange model, the demand for capital and therefore investment depends in the long run on the cost of capital. The intuition is in line with standard microeconomic theory: companies choose the combination of capital and labour that maximises their profit. A rise in the cost of capital leads firms to substitute labour for capital and pushes down investment. The user cost of capital is composed of the depreciation of capital, the long-term interest rate on government debt and the terms of the risk premium between government bonds and corporate loans, while the long-term elasticity of investment to this user cost is estimated to be 0.44. Assuming a 10% capital depreciation rate, initial nominal rates at 0, and ignoring any risk premia, a 1% increase in the interest rate translates in the long run into a 5% decrease in investment. The second, much less intuitive channel plays a key role in this variant and explains in particular the response of prices and exports. An increase in the cost of capital means higher production costs for business. Firms pass on these higher costs in their selling prices, leading to higher inflation and lower competitiveness. Portier, Beaudry and Hou (2022) recently explored this positive impact of a rise in interest rates on prices via the cost of capital channel. Note that this effect is difficult to detect using more agnostic empirical methods (unrestricted VAR models, local projections). While these sometimes show positive effects in terms of how a rise in rates impacts prices, the effect is usually either insignificant or clearly negative over longer time horizons (see for example Miranda-Agrippino and Ricco, 2021).
The FR-BDF model
Compared to Mésange, one of the important features of the FR BDF model is the way it treats agents’ expectations. This specificity explains why two interest rates intervene in the dynamics of the model. The short-term interest rate, determined by the European Central Bank, affects agents’ expectations, while the long-term interest rate on public bonds affects the long-term demand for production factors. The long-term elasticity of investment to the cost of capital is 0.5, which is slightly higher than in Mésange. The FR BDF model does not incorporate systematic relationships between long and short rates. To generate the effect of a rate shock in the model, it is therefore necessary to add two distinct analytical variants, the first simulating the impact of a permanent rise in the short-term rate, the second the impact of a rise in the long-term rate. These two variants are available in Aldama and Ouvrard (2020). The effects of a rate shock are much weaker than in Mésange. After 3 years, real GDP decreases by 0.3%, against 0.9% in Mésange. This is due in particular to a much smaller reduction in GFCF (-1.9% compared to -3.4% after 3 years in Mésange). The effects on prices are more in line with the usual Keynesian intuition, with a 0.2% fall in the GDP deflator after 3 years. The resulting improvement in competitiveness leads to an increase in exports of 0.2% after 3 years (compared to a 0.2% decrease in Mésange). There are two main reasons for these differences. First, the transmission channel of the cost of capital to prices is neutralised in the FR BDF model. While value-added prices are determined by the cost of production factors and a constant markup, as in Mésange, the cost of the capital factor that enters the price equation is not the user cost of capital but the marginal return to capital. Second, investment reacts much less strongly in the short term to the growth in value added in FR-BDF and is characterised by greater inertia. The negative investment shock therefore spreads more slowly.
The e-mod model
The impact of a rate shock in the version of the e-mod model developed by Heyer and Timbeau (2006) is closer to the results of FR BDF than to Mésange. However, the economic mechanism is different. The interest rate shock is transmitted via a fall in asset prices, particularly property prices, which leads to a reduction in consumption via a wealth effect. After 3 years, real GDP falls by 0.4%, a fall that is driven by the reduction in household spending (consumption and investment) (-0.6%) and, to a lesser extent, in business investment (-1.2%)[2]. As in FR-BDF, the rate shock negatively impacts prices. The GDP and household consumption deflators fall by 0.1%.
What does this overview tell us?
The main transmission channel of a rate shock in macroeconometric models involves the user cost of capital and business and household investment. The magnitude of this negative effect on investment depends on the long-run elasticity of the demand for capital to its user cost. These models estimate this elasticity econometrically. While criticisms can be made of the estimation methods, the value ultimately adopted (on the order of 0.5) seems plausible relative to other estimation methods (for example, a meta-study by Gechert et al., 2022, estimates it at 0.3) and implies moderate substitutability between production factors. It is also possible that the rate shock impacts household consumption via wealth effects, even if this channel remains controversial. In addition to these primary effects on aggregate demand, there are multiplier and accelerator effects that also vary between the models, adding to the uncertainty. We find the channel of production costs, which has a certain importance in the dynamics of the Mésange model, implausible. This leads us to retain in this paper the results of Aldama and Ouvrard (2020) and Heyer and Timbeau (2006).
The impact of monetary tightening on economic activity will depend not only on the response of the economy to a generic shock but also on the size of the current shock. In the October 2022 OFCE forecast, the one-year interest rate hike is projected to be 300 basis points, but this hike cannot be used as is. First, this rise is not coming as a complete surprise. Interest rates fell to very low levels during the Covid-19 crisis, and normalisation was expected to start by 2022, albeit at a very gradual pace. Second, this is a rise in the nominal rate. The relevant interest rate for the transmission channels of monetary policy as they appear in macroeconometric models is the real rate. This would not pose a problem if the rate hike were a pure monetary policy shock, i.e. if the central bankers had decided overnight to raise rates without any reason. But the rise that we are experiencing is a response to an inflationary shock, a shock that is affecting real interest rates independently of any changes in the nominal rate. The solution adopted by the OFCE in its October 2022 forecasts[3] was to retain the change in the real rate using certain measures of inflation expectations. This leads to a rate shock of around 2%.
On the basis of the two variants that we have chosen, a rate shock of around 2% could, all else being equal, cause French GDP to fall between 0.6% and 0.8% by 2024/2025. The impact on prices would be negative but modest, between 0.3% and 0.4%. This estimate obviously remains very uncertain. As explained in the previous paragraph, calculating the magnitude of the shock itself requires making major assumptions. The models used are estimated with limited information and therefore have potentially broad confidence intervals. More generally, the validity of this estimate of the effects of a rate shock is contingent on the validity of the models used.
Bibliography
Aldama P. and J.-F. Ouvrard, 2020, “Variantes analytiques du modèle de prévision et simulation de la Banque de France pour la France” [Analytical variants of the Banque de France forecasting and simulation model for France], Document de travail Banque de France, no. 750.
Bardadji J., B. Campagne, M. Khder, Q. Lafféter and O. Simon, 2017, “Le modèle macroéconométrique Mésange : réestimation et nouveautés” [The Mesange macroeconometric model: Re-estimation and innovations], Document de travail INSEE.
Beaudry P., S. Hou and F. Portier, 2020, “Monetary policy when the Philips Curve is quite flat”, CEPR discussion paper.
Gechert S., T. Havranek, Z. Irsova and D. Kolcunova, 2022, “Measuring capital-labor substitution: The importance of method choices and publication bias”, Review of Economic Dynamics, no. 45, pp. 55-82.
Heyer E. and X. Timbeau, 2006, “Immobilier et politique monétaire” [Real estate and monetary policy], Revue de l’OFCE, no. 96, pp. 115-151.
Miranda-Agrippino S. and G. Ricco, 2021, “The transmission of monetary policy shocks”, American Economic Journal : Macroeconomics, vol. 13, no. 3, pp. 74-107.
OFCE, E. Heyer and X. Timbeau (dirs.), 2022, “Perspectives 2022-2023 pour l’économie mondiale et la zone euro”, [2022-2023 Forecast for the Global Economy and the Euro Zone], Revue de l’OFCE, no. 178.
[1] See Table 2 in Appendix 1 of the OFCE forecast in the section Tour du monde de la situation conjoncturelle, [Overview of the economic situation], OFCE Forecasting and Analysis Department, under the direction of E. Heyer and X. Timbeau.
[2] These figures are obtained by dividing the results presented in Heyer and Timbeau (2006) by two, as the authors simulated an interest rate rise of 200 bps. As the e-mod model is not completely linear, the results are an approximation.
[3] See Box 2 in Perspectives 2022-2023 pour l’économie mondiale et la zone euro, [2022-2023 Forecast for the Global Economy and the Euro Zone], E. Heyer and X.Timbeau (dirs.).