L’année 2022 a été marquée par une très forte poussée inflationniste aux États-Unis et en zone euro. Fin octobre, le taux d’inflation atteint 7,7% sur un an aux États-Unis, 10,6% en zone euro et 7,1% en France, soit entre 5 et 8 points au-dessus des cibles d’inflation de la Réserve fédérale américaine (Fed) et de la Banque centrale européenne. En réponse, les deux banques centrales ont opéré un resserrement monétaire de grande ampleur. Le taux d’intérêt directeur de la Fed est passé de 0% en mars 2022 à 4% en novembre 2022. Si la hausse du taux directeur de la BCE a été pour le moment plus mesurée, les taux longs sur les dettes publiques des pays européens ont connu une très forte progression, gagnant entre 250 et 300 points de base en un an en France ou en Allemagne, voire davantage dans les pays de la zone euro où le risque sur la dette publique est perçu comme plus élevé. Cette hausse est proche de celle anticipée pour les taux courts en 2023. Ainsi, l’OFCE prévoit que le taux directeur de la BCE atteindra 3% au troisième trimestre 2023[1].
Estimer l’impact qu’aura ce resserrement sur l’activité économique est difficile. La transmission d’un choc monétaire sur le reste de l’économie fait l’objet d’une littérature très riche utilisant des méthodes conceptuellement proches, voire équivalentes, mais dont les résultats peuvent fortement varier en pratique. Nous nous intéressons ici particulièrement à l’impact d’un choc de taux dans les modèles macro-économétriques de l’économie française. Pour ce tour d’horizon, nous retenons trois modèles : le modèle Mésange codéveloppé par la DG trésor et l’INSEE (voir Bardaji et al., 2017), le modèle FR BDF de la Banque de France (voir Lemoine et al. 2019 et Aldama et Ouvrard 2020 pour le cahier de variantes) ainsi que la spécification du modèle emod de l’OFCE utilisée dans Heyer et Timbeau (2006).
Qu’est-ce qu’un modèle macroéconométrique ?
Les modèles macroéconométriques représentent la classe la plus ancienne des modèles macroéconomiques. Ils combinent relations (ou équations) comptables et équations de comportement estimées pour former des prédictions sur la réponse de l’économie aux chocs. Les grandes variables macro-économiques (salaire, prix, consommation des ménages, investissement, emploi) sont exprimées sous la forme d’équations à correction d’erreurs. Á long terme, elles convergent vers une certaine cible, déterminée par la théorie économique. Ainsi la dépense de consommation des ménages convergera sur le long terme vers une certaine fraction du revenu disponible des ménages. En revanche, le comportement à court terme est laissé beaucoup plus libre de manière à obtenir de bonnes performances en prévision. Le taux d’intérêt intervient essentiellement à long terme. L’impact d’un choc de taux est limité dans un premier temps et devient plus important au fur et à mesure que l’écart entre les variables et leurs cibles de long terme se comble.
Le modèle Mésange
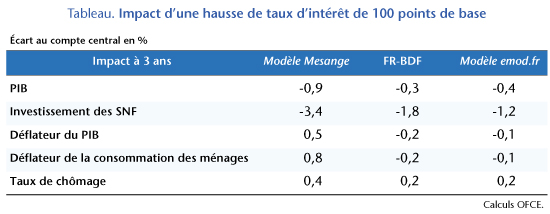
Nous considérons la variante publiée dans Bardaji et al. (2017). Les résultats sont résumés dans le tableau 1. Un choc monétaire de 100 points de base (ou 1%) se traduit par une baisse du PIB de 0,2% au bout d’un an, 0,8% au bout de trois ans et de 3% à long terme. Cette baisse s’explique notamment par la forte chute de l’investissement : -2,7% au bout de 3 ans (-3,4% pour la FBCF des entreprises non financières) et -5,5% à long terme mais toutes les composantes de la demande globale sont affectées négativement, y compris les exportations qui chutent de 3,3% à long terme. De manière étonnante, le resserrement monétaire se traduit par une hausse des prix dans le modèle Mésange. Les prix de valeur ajoutée marchande progressent ainsi de 0,1% au bout d’un an, 0,8% au bout de 3 ans et de plus de 6% à long terme ! Cette hausse des prix dégrade la compétitivité de l’économie, ce qui explique le recul des exportations. Deux canaux de transmission sont à l’œuvre. Le premier est l’impact négatif direct d’une hausse des taux d’intérêt sur l’investissement des entreprises. Dans le modèle Mésange, la demande de capital et donc l’investissement dépend à long terme du coût du capital. L’intuition est celle de la théorie micro-économique standard : les entreprises choisissent la combinaison de capital et de travail qui maximise leur profit. Une hausse du coût du capital incite les entreprises à substituer du travail au capital et réduit l’investissement. Le coût d’usage du capital est composé de la dépréciation du capital, du taux d’intérêt de long terme sur la dette publique et de termes de primes de risques entre les obligations d’État et les prêts aux entreprises, tandis que l’élasticité de long terme de l’investissement à ce coût d’usage est estimée sur le long terme à 0,44. Sous l’hypothèse d’un taux de dépréciation de capital de 10%, des taux nominaux initiaux à 0 et en faisant abstraction des primes de risque, une hausse de 1% du taux d’intérêt se traduit à long terme par une baisse de l’investissement de 5%. Le deuxième canal, beaucoup moins intuitif, joue un rôle clé dans cette variante et explique en particulier la réponse des prix et des exportations. Une hausse du coût du capital représente une hausse des coûts de production pour les entreprises. Celles-ci répercutent cette hausse des coûts dans leur prix de vente, d’où un effet inflationniste et une baisse de la compétitivité. Cet effet positif d’une hausse des taux d’intérêt sur les prix via le canal du coût du capital a été exploré récemment par Portier, Beaudry et Hou (2022). Il convient cependant de souligner que cet effet est difficilement détecté par les méthodes empiriques plus agnostiques (modèles VAR sans restriction, projections locales). Si des effets positifs en impact d’une hausse des taux sur les prix sont parfois obtenus, l’effet devient le plus souvent soit non significatif soit clairement négatif sur des horizons plus longs (voir par exemple Miranda-Agrippino et Ricco, 2021).
Le modèle FR-BDF
Par rapport à Mésange, l’une des spécificités importantes de FR BDF est le traitement des anticipations des agents dans le modèle. Cette spécificité explique que deux taux d’intérêt interviennent dans la dynamique du modèle. Le taux d’intérêt de court terme, déterminée par la Banque centrale européenne, affecte les anticipations des agents tandis que le taux d’intérêt de long terme des obligations publiques joue sur la demande de facteurs de production à long terme. L’élasticité de long terme de l’investissement au coût du capital est de 0,5, légèrement supérieure à celle de Mésange. Le modèle n’incorpore pas de relations systématiques entre les taux longs et les taux courts. Pour obtenir l’effet d’un choc de taux dans le modèle, il convient donc d’additionner deux variantes analytiques distinctes, la première simulant l’impact d’une hausse permanente du taux court, la seconde simulant l’impact d’une hausse du taux long. Ces deux variantes sont disponibles dans Aldama et Ouvrard (2020). Les effets d’un choc de taux sont beaucoup plus faibles que dans Mésange. Au bout de 3 ans, le PIB en volume diminue de 0,3% contre 0,9% dans Mésange. Cela s’explique en particulier par une baisse bien plus faible de la FBCF des entreprises (-1,9% contre -3,4% au bout de 3 ans dans Mésange). Les effets sur les prix sont plus conformes à l’intuition keynesienne habituelle avec une baisse du déflateur du PIB de 0,2% au bout de 3 ans. L’amélioration de la compétitivité qui en résulte permet une hausse des exportations de 0,2% au bout de 3 ans (contre une baisse de 0,2% dans Mésange). Ces différences s’expliquent principalement par deux éléments. Tout d’abord, le canal de transmission du coût du capital vers les prix est neutralisé dans le modèle FR BDF. Si les prix de valeur ajoutée sont déterminés par le coût des facteurs de production et un markup constant comme dans Mésange, le coût du facteur capital qui entre dans l’équation de prix n’est pas le coût d’usage du capital mais le rendement marginal du capital. Ensuite, l’investissement réagit beaucoup moins fortement à court terme à la croissance de la valeur ajoutée dans FR-BDF, et se comporte de manière plus inertielle. Le choc négatif d’investissement se diffuse donc plus lentement.
Le modèle emod
L’impact d’un choc de taux dans la version du modèle emod développée par Heyer et Timbeau (2006) est plus proche des résultats de FR BDF que de Mésange. Le mécanisme économique est cependant différent. Le choc de taux se transmet via une baisse du prix des actifs, notamment immobiliers, ce qui induit une réduction de la consommation via un effet richesse. Après 3 ans, le PIB en volume diminue de 0,4 %, une baisse tirée par la réduction de la dépense (consommation et investissement) des ménages (-0,6%) et dans une moindre mesure de l’investissement des entreprises (-1,2%)[2]. Comme dans FR-BDF, le choc de taux a un impact négatif sur les prix. Les déflateurs du PIB et de la consommation des ménages baissent de 0,1%.
Que retenir de ce tour d’horizon ?
Le principal canal de transmission d’un choc de taux dans les modèles macro-économétriques passe par le coût d’usage du capital et l’investissement des firmes et des ménages. L’ampleur de cet effet négatif sur l’investissement dépend de l’élasticité de long terme de la demande de capital à son coût d’usage. Dans ces modèles, cette élasticité fait l’objet d’une estimation économétrique. Les méthodes d’estimation ne sont pas exemptes de critiques mais la valeur finalement retenue (de l’ordre de 0,5) semble plausible au regard des autres méthodes d’estimations (ainsi une méta-étude de Gechert et al., 2022, l’estime à 0,3) et implique une substituabilité modérée entre les facteurs de production. Un impact du choc du taux sur la consommation des ménages via des effets richesses est également possible même si ce canal demeure controversé. Á ces effets primaires sur la demande agrégée s’ajoutent des effets multiplicateurs et d’accélérateur qui varient également selon les modèles, rajoutant un facteur d’incertitude supplémentaire. Le canal des coûts de production qui a une certaine importance dans la dynamique du modèle Mésange nous apparaît comme peu plausible. Cela nous conduit à retenir dans ce billet les résultats d’Aldama et Ouvrard (2020) et de Heyer et Timbeau (2006).
L’impact du resserrement monétaire sur l’activité économique dépendra non seulement de la réponse de l’économie à un choc générique mais aussi de l’ampleur du choc actuel. Dans la prévision d’octobre 2022 de l’OFCE, la hausse des taux d’intérêt sur un an est prévue pour être de 300 points de base mais cette hausse ne peut être utilisée telle quelle. D’une part, cette hausse n’est pas une complète surprise. Les taux d’intérêt ont atteint des niveaux très bas lors de la crise de la Covid-19 et un début de normalisation était attendu pour 2022, certes à un rythme très progressif. D’autre part, il s’agit de la hausse du taux nominal. Le taux d’intérêt pertinent pour les canaux de transmission de la politique monétaire tels qu’ils apparaissent dans les modèles macro-économétriques est le taux réel. Cela ne poserait pas de problèmes si la hausse des taux était un pur choc de politique monétaire, c’est-à-dire si les banquiers centraux avaient décidé du jour au lendemain d’augmenter les taux sans raison. Mais la hausse que nous connaissons est une réponse à un choc inflationniste, choc qui affecte le taux d’intérêt réel indépendamment de l’évolution du taux d’intérêt nominal. La solution adoptée par l’OFCEdans ses prévisions d’octobre 2022[3] est de retenir l’évolution du taux réel en utilisant certaines mesures des anticipations d’inflation. Cela conduit à un choc de taux de l’ordre de 2%.
Sur la base des deux variantes que nous retenons, un choc de taux de l’ordre de 2% pourrait provoquer, toutes choses égales par ailleurs, une baisse du PIB français comprise entre 0,6 et 0,8% à l’horizon 2024/2025. L’impact sur les prix serait négatif mais demeurerait modeste, compris entre 0,3 et 0,4%. Cette estimation demeure évidemment très incertaine. Comme expliqué dans le paragraphe précédent, calculer l’ampleur du choc elle-même requiert de réaliser des hypothèses importantes. Les modèles utilisés sont estimés avec une information limitée et donc des intervalles de confiance potentiellement larges. De manière plus générale, la validité de cette estimation des effets d’un choc de taux est contingente à la validité des modèles retenus.
Bibliographie
Aldama P. et J.-F. Ouvrard, 2020, « Variantes analytiques du modèle de prévision et simulation de la Banque de France pour la France », Document de travail Banque de France, n° 750.
Bardadji J., B. Campagne, M. Khder, Q. Lafféter et O. Simon, 2017, « Le modèle macroéconométrique Mésange : réestimation et nouveautés», Document de travail INSEE.
Beaudry P., S. Hou et F. Portier, 2020, « Monetary policy when the Philips Curve is quite flat », CEPR discussion paper.
Gechert S., T. Havranek, Z. Irsova et D. Kolcunova, 2022, « Measuring capital-labor substitution: The importance of method choices and publication bias », Review of Economic Dynamics, n° 45, pp. 55-82.
Heyer E. et X. Timbeau, 2006, « Immobilier et politique monétaire », Revue de l’OFCE, n° 96, pp. 115-151.
Miranda-Agrippino S. et G. Ricco, 2021, « The transmission of monetary policy shocks », American Economic Journal : Macroeconomics, vol. 13, n° 3, pp. 74-107.
OFCE, E. Heyer et X. Timbeau (dirs.), 2022, « Perspectives 2022-2023 pour l’économie mondiale et la zone euro », Revue de l’OFCE, n° 178.
[1] Voir dans la prévision de l’OFCE le tableau 2 de l’annexe 1 de la partie Tour du monde de la situation conjoncturelle, Département Analyses et Prévisions, sous la direction d’E. Heyer et X. Timbeau.
[2] Ces chiffres sont obtenus en divisant les résultats présentés dans Heyer et Timbeau (2006) par deux, les auteurs ayant simulé une hausse des taux d’intérêt de 200 bps. Le modèle emod n’étant pas complétement linéaire, ces résultats constituent une approximation.
[3] Voir l’encadré 2 de Perspectives 2022-2023 pour l’économie mondiale et la zone euro, sous la direction d’E. Heyer et X.Timbeau.