Afin d’établir une stratégie pour faire face à l’épidémie de Covid-19, le décideur public nécessite des données pour prendre des décisions. Or nombre des paramètres, pourtant indispensables, ne sont pas directement observables. Selon Santé Publique France, au 25 avril à 14 heures, il y avait 124 114 cas détectés de Covid-19 en France dont 87 524 cas ayant abouti à une hospitalisation et 22 614 décès seraient liés à la pathologie. Selon ces données brutes seulement 0,2 % de la population aurait été contaminée à ce jour par le virus, plus de 7 patients sur 10 nécessiteraient une hospitalisation et quasiment 2 malades sur 10 décèderaient. Pour de bonnes raisons, personne n’utilise les données brutes de cette façon aussi basique : les cas détectés le sont parmi les personnes affichant les symptômes les plus graves, négligeant ainsi un grand nombre de cas asymptomatiques et bénins, ce qui entraîne un biais statistique qui empêche de généraliser les résultats à l’ensemble de la population.
La science économique a développé des outils pour traiter des données générées de façon non aléatoire et même pour tirer des conclusions lorsque les données nécessaires sont tout simplement inexistantes. Charles Manski[1] et Francesca Molinari ont publié un article où ils essayent de borner des paramètres clés de l’épidémie, exclusivement à partir des données disponibles. Pour ceci, ils utilisent l’approche de l’identification partielle, qui vise à établir des résultats fondés sur les données disponibles en formulant le moins d’hypothèses possibles. Dans ce post de blog, la méthodologie proposée par les auteurs est appliquée aux données françaises.
Deux sources d’incertitude : la qualité des tests et la stratégie de test
Partant des définitions basiques des probabilités, Manski et Molinari donnent la formule exacte qui permet de calculer la probabilité pour une personne d’être contaminée (voir encadré). Hélas certaines des données nécessaires pour réaliser le calcul précédant sont inconnues. Deux facteurs majeurs empêchent d’utiliser directement les données brutes publiées par les autorités sanitaires :
- La performance des tests de diagnostic et plus particulièrement l’ampleur des faux-négatifs.
- La stratégie de tests qui empêche de tirer des conclusions directes sur la part de la population contaminée qui n’a pas été testée à partir des taux de positivité des tests réalisés.
Ces deux sources d’incertitude sont de nature différente. La première source est en rapport avec la nouveauté du virus. Elle ne peut être levée que par la recherche médicale. Manski et Molinari considèrent que cette incertitude est bornée par la littérature médicale. La part des faux-négatifs s’établirait entre 10 % et 40 % selon les études auxquelles ils ont eu accès. La deuxième source d’ignorance est en lien avec la stratégie de test. En règle générale, les tests ont été réservés aux malades affichant les symptômes les plus graves. De ce fait, la probabilité d’être contaminé est plus élevée chez les personnes testées que dans la population n’ayant pas été testée. Si un échantillon représentatif de la population avait été testé, cette source d’incertitude pourrait être éliminée.
Selon Manski et Molinari, la part de la population ayant été contaminée par le Covid-19 peut être circonscrite à l’aide des données brutes, les bornes sur le nombre de faux-négatifs et par l’hypothèse très générale posée sur la stratégie de test disant que la probabilité d’être contaminé est supérieure chez les personnes testées aux individus non testés[2] :

Il est très important de remarquer que ces intervalles donnent toutes les valeurs du paramètre d’intérêt compatibles avec les données brutes disponibles et les maigres hypothèses posées. Tout chiffre situé à l’intérieur de l’intervalle est également compatible avec les données brutes.
Les méthodes de l’identification partielles sont peu utiles pour connaître la part de la population contaminée à ce jour en France…
Selon le dernier point épidémiologique hebdomadaire publié par Santé Publique France, au 19 avril, 457 287 tests avaient été réalisés en milieu hospitalier depuis le 24 février. Par ailleurs, 141 298 tests avaient été réalisés en ville. Ainsi, près de 600 000 tests auraient été réalisés depuis le début de l’épidémie (soit un peu moins de 1 % de la population).
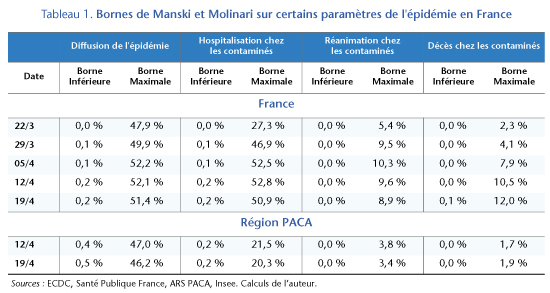
Les données disponibles à ce jour sont très peu informatives sur l’étendue de la population qui a déjà été contaminée par le virus. Au 19 avril, les données disponibles sont compatibles avec une part de la population contaminée comprise entre 0,2 % et 51,4 %. La largeur de l’intervalle des valeurs du paramètre compatible avec les données suggère clairement que l’on ne peut pas trancher exclusivement à l’aide de celles-ci (tableau 1).
En grande partie, la largeur de cet intervalle s’explique par le faible nombre de tests réalisés. Par exemple, si l’on néglige l’incertitude portant sur le taux de faux-négatifs et l’on choisit une valeur centrale de 25 %, l’intervalle serait plus resserré mais toujours peu informatif : la part de la population contaminée pourrait être entre 0,3 % et 39,2 %.
… mais peuvent donner des bornes plus resserrées pour les paramètres de dangerosité de la maladie…
Avec les données publiées par Santé Publique France il est aussi possible de borner certains paramètres clés sur la dangerosité du virus : (i) la part des cas nécessitant une hospitalisation (ii) la part des cas nécessitant de soins de réanimation et (iii) la part des contaminés qui décèdent. D’une part, la part des cas graves dans la population est directement observable tandis que d’autre part, la proportion de la population contaminée peut être bornée par les résultats – même peu informatifs − de la section antérieure. Le ratio entre les cas graves observés et la borne maximale (respectivement minimale) inférée de la population contaminée donne la borne inférieure (resp. maximale) de la part des cas graves de Covid-19 parmi les personnes contaminées.
Dans ce contexte, la part des cas de Covid-19 nécessitant une hospitalisation serait comprise entre [0,2 % et 51 %] ; celle des cas nécessitant de soins de réanimation serait comprise [0,04 % et 8,9 %] et la probabilité de décès serait comprise entre [0,06 % et 12 %]. Il est intéressant de noter que même les bornes supérieures de ces intervalles sont bien plus basses par rapport aux données brutes observées : 73 % des cas détectés se sont soldés par une hospitalisation, 13 % par un passage en réanimation et 17 % par un décès.
Si l’on utilise les données de la région PACA[3], où une part plus importante de la population a été testée (2,6 % de la population), les intervalles pour les paramètres de dangerosité du Covid-19 sont nettement plus étroits : entre 0,2 % et 20 % des cas aboutiraient à une hospitalisation ; entre 0,04 % et 3,4 % des cas nécessiteraient de soins intensifs et entre 0,02 % et 1,9 % des cas seraient mortels. Ces résultats, obtenus sur une population qui a été plus largement testée, sont compatibles avec les résultats de l’étude épidémiologique de l’Institut Pasteur citée-ci-dessus, qui repose sur des hypothèses plus fortes.
…notamment lorsqu’on élargit la vue aux pays ayant réalisé le plus de tests
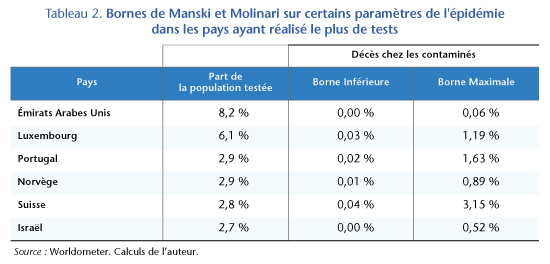
Avec son statut de pandémie, de nombreuses données sont largement disponibles pour de nombreux pays. Bien que chaque pays ait des stratégies de test différentes, la généralité de l’hypothèse posée dans les sections précédentes permet d’appliquer le cadre d’analyse aux différents pays. Parmi les 60 pays ayant déjà connu plus de 50 décès liés au Covid-19, la France se situe à la 29e place en termes de la part de la population testée. Que nous disent les résultats des pays qui ont le plus testé leur population sur le degré de létalité de la maladie ?
Au 24 avril, les Émirats arabes unis ont testé 8,2 % de la population, le Luxembourg 6,1 %, le Portugal et la Norvège 2,9 %, la Suisse 2,8 % et Israël 2,7 %. Tous ces pays ont testé leur population plus largement que la région PACA. En appliquant les bornes de Manski et Molinari nous pouvons trouver des bornes supérieures du taux de mortalité des infectés au Covid-19 encore plus basses que celles qu’on obtient à partir des données françaises, sauf en Suisse où les données ne permettent pas d’exclure un taux de mortalité allant jusqu’à 3,15 %. Dans les autres pays de cet échantillon, la part de cas mortels est en général proche à 1 % (tableau 2). Néanmoins, ces résultats peuvent être expliqués par les idiosyncrasies locales et doivent être pris avec précaution.
Une meilleure connaissance de la part des cas asymptomatiques pour réduire l’incertitude
Comme nous l’avons vu, les données brutes disponibles à ce jour sont insuffisantes pour pouvoir donner des ordres de grandeur utiles à la décision publique sur l’étendue de l’épidémie du Covid-19 en France. Malgré cela l’approche de l’identification partielle fournit des bornes pour les indicateurs de dangerosité du virus crédibles et utiles. Néanmoins, il est clair qu’une meilleure connaissance sur la pathologie permettrait de mieux borner les évaluations. En particulier, une meilleure connaissance concernant la part des cas asymptomatiques serait particulièrement utile[4].
Heureusement, en attendant d’avoir des données plus nombreuses, les épidémiologistes de l’Institut Pasteur, en modélisant le mode de diffusion de la maladie, donnent des résultats plus précis : ils tablent sur un chiffre de 5,7 % de la population française qui aurait déjà été contaminée par le virus. Dans ce contexte, 0,53 % des contaminés courent un risque de décès en lien avec le Covid-19, un chiffre en ligne avec nos évaluations basées sur les pays ayant largement testé leur population.
Au final trois éléments semblent capitaux pour réduire l’incertitude : développer le nombre de tests avec éventuellement des échantillons aléatoires représentatifs de la population, améliorer la qualité des tests afin de réduire le nombre des faux-négatifs et améliorer nos connaissances sur le virus. Le projet EpiCOV porté par l’Inserm et la Drees semble faire un pas dans la bonne direction et devrait permettre d’améliorer sensiblement notre connaissance sur le Covid-19.
| Encadré : La formule de Manski et Molinari pour calculer la part de la population contaminée par le Covid-19 À partir de la formule des probabilités totales et des définitions des probabilités jointes, conditionnelles et marginales, Manski et Molinair donnent la formule qui permettrait de calculer la part de la population contaminée par le Covid-19 : P(Cd=1)=P(Cd=1|Rd=1).P(Rd=1|Td=1).P(Td=1)+P(Cd=1|Td=0).P(Td=0)+P(Cd=1|Td=1,Rd=0).P(Rd=0|Td=1.P(Td=1) On note Cd=1 lorsqu’une personne a déjà été infectée par le virus à une date d et Cd=0 lorsqu’une personne n’a pas été infectée. Les auteurs cherchent à connaître la part de la population ayant été contaminée, qui est égale au niveau individuel à la probabilité d’avoir été contaminé, notée P(Cd=1). Malheureusement, cette grandeur n’est pas directement observable. Par contre les autorités sanitaires fournissent des données qui peuvent informer sur cette grandeur, en particulier les personnes testées (Td=1) et les cas détectés (Rd=1). Trois termes de cette égalité ne sont pas observables : la part des cas détectés qui sont effectivement contaminés (le terme P(Cd=1|Rd=1 )), les auteurs jugent, sur la base de la littérature médicale, que la quasi-totalité les tests positifs sont des vrais positifs alors ce terme ne pose pas de problème dans l’analyse ; la part des personnes contaminées, qui ont été testées mais dont le test a donné un résultat négatif [P(Cd=1|Td=1,Rd=0)], ce terme correspond aux faux-négatifs ; enfin, la part des personnes contaminées, mais qui n’ont pas été détectées faute de test [terme P(Cd=1|Td=0)]. |
[1] Dans ces travaux Manski a essayé de faire apparaître l’apport « pur » des données dans les résultats empiriques en sciences sociales. Pour Manski, lorsqu’on s’intéresse à un paramètre dans un modèle, les données toutes seules ne peuvent identifier qu’un intervalle de valeurs compatibles avec les données. Pour réduire la largeur de cet intervalle, des hypothèses — de comportement, de forme fonctionnelle, de loi statistique sous-jacente — peuvent être posées afin de réduire la largeur de l’intervalle. Seulement en posant une grande quantité d’hypothèses on peut arriver à l’identification ponctuelle du paramètre. Voir Manski (1995), « Identification Problems in the Social Sciences », Harvard, 1995, pour une introduction à ses travaux.
[2] Le lecteur pourra se référer à l’article de Manski et Molinari pour connaître le détail des calculs, dont la compréhension ne nécessite qu’une connaissance relativement basique du calcul des probabilités.
[3] Il aurait été souhaitable de réaliser ce type de travail pour les régions où le virus a largement circulé (Grand Est, Île-de-France) mais les données publiées par les ARS de ces régions ne permettent pas de calculer l’ensemble des données nécessaires pour ce type de calcul.
[4] Manski et Molinari (2020) fournissent les formules permettant de modifier les bornes des intervalles lorsqu’on a des évaluations précises de la part de cas asymptomatiques. Par exemple, on peut utiliser le taux de 17 % de cas asymptomatiques issu de l’étude de l’Institut Pasteur portant sur un lycée de Crépy-en-Valois. Dans ce cas, les données publiées par l’Agence Régionale de Santé de la région PACA suggèrent que la part des cas de Covid-19 nécessitant une hospitalisation serait au maximum de 16,8 %, celle des cas nécessitant des soins de réanimation serait au maximum de 2,9 % et celle des cas mortels au maximum de 1,6 %.


Poster un Commentaire